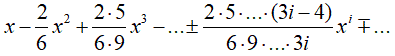
Перед нами стоит задача вычислить сумму бесконечного ряда. В принципе, написать бесконечный цикл возможно. В языке Паскаль это делается следующим образом:
while true do begin ... end;

Поскольку условие всегда истинно, цикл будет выполняться бесконечно. Однако хоть и существуют алгоритмы, где использование бесконечного цикла имело бы смысл, наша задача не предполагает бесконечной работы алгоритма. Вычисления должны быть сделаны за конечное время. Кроме того, числа в компьютере представляются с некоторой точностью, поэтому бесконечные вычисления в любом случае бессмысленны, поскольку невозможно превысить точность, определяемую способом представления вещественных чисел в памяти компьютера.

Если ряд сходится, и i-ое слагаемое меньше некоторого числа ε, называемого точностью вычислений, то и сумма всех остальных слагаемых с номерами i + 1, …, ∞ будет меньше числа ε. Доказывать это утверждение не будем, примем как аксиому. Поэтому если i-ое слагаемое меньше числа ε, то остальные слагаемые можно отбросить и считать, что желательная точность вычислений достигнута.

Таким образом, мы от бесконечного ряда, в принципе, перешли к конечному. Однако сколько слагаемых потребуется для достижения заданной точности, не известно. И вычислить это число не представляется возможным. Поэтому в данном случае невозможно использовать параметрический цикл, который является циклом с известным числом повторений. Действительно, для того чтобы использовать параметрический цикл, нужно указать начальное значение параметра (тут можно взять 1) и конечное значение параметра – подставить некоторую константу или переменную. Константу использовать вообще бессмысленно, переменной тоже должно быть присвоено некоторое разумное значение, а вычислить количество необходимых слагаемых мы, как уже было сказано, не можем.

С другой стороны, циклы «пока» и «до» не требуют указания точного количества итераций. Нужно лишь подставить условие, и цикл будет выполняться, пока условие не станет ложным (для цикла «пока») или истинным (для цикла «до»), т.е. циклы «пока» и «до» являются циклами с неизвестным числом повторений. В нашем случае, в принципе, существует теоретическая возможность вычислить необходимое количество слагаемых, но могут встречаться ситуации, когда такая возможность не существует даже теоретически. Например:
readln(a, b); while a > b do readln(a, b);

Когда пользователь введёт такие числа, что a будет больше b, вычислить никак невозможно. Поэтому циклы «пока» и «до» – это циклы с совершенно неизвестным числом повторений.

Таким образом, мы определили, что в задаче вычисления суммы ряда необходимо использовать следующий цикл:
while abs(a) > e do ...

Здесь e – заданная точность, a – значение очередного слагаемого, оно берётся по модулю, т.к. ряд знакопеременный.

В формулах вычисления слагаемого встречаются степени, факториалы, произведения многих сомножителей. Получается, что для вычисления суммы ряда требуется много операций. Однако если внимательно посмотреть на слагаемые, можно выделить некоторые закономерности, которые позволят сократить количество вычислений.

Рассмотрим ряд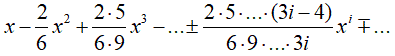

Произведём некоторые вычисления.

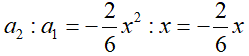
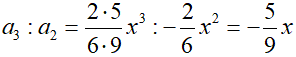
Мы видим, что в обоих случаях при делении i-ого слагаемого на (i – 1)-ое, получается похожее выражение – x в первой степени, одно число в числителе и одно число в знаменателе. Таким образом, зная (i – 1)-ое слагаемое можно будет получить i-ое слагаемое, если мы сможем выразить числа, стоящие в числителе и знаменателе, через номер слагаемого. Произведём те же вычисления в общем виде.

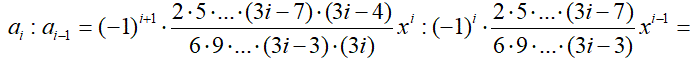
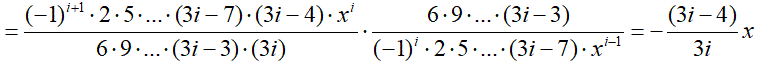
Таким образом, мы получили формулу, которая позволяет перейти от (i – 1)-ого слагаемого к i-ому. Эта формула называется рекуррентным соотношением.

При вычислении рекуррентных соотношений надо понимать, что в рядах, подобных рассмотренному, i-ое слагаемое обычно имеет в числителе и знаменателе на один сомножитель больше, чем (i – 1)-ое слагаемое. Поэтому все сомножители (i – 1)-ого слагаемого сокращаются с соответствующими сомножителями i-ого слагаемого, а от i-ого слагаемого остаются по одному сомножителю в числителе и знаменателе. Также обычно остаётся x в некоторой степени и –1.

Аналогично сокращаются факториалы, которые, собственно, также являются произведениями нескольких сомножителей:

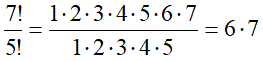
Или в общем виде:

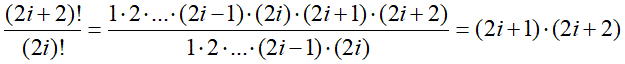
Таким образом, в программе необходимо сначала присвоить начальные значения переменным для номера слагаемого, самого слагаемого и суммы ряда, затем в цикле вычисляется следующее слагаемое путём умножения предыдущего слагаемого на рекуррентное соотношение, новое слагаемое добавляется в общую сумму и номер слагаемого увеличивается на 1.

Большинство рядов сходится при условии |x| < 1. Также надо вводить правильные значения точности, которая в данной задаче никак не может быть равна 10 или даже 1, а должна быть малым положительным числом, например, 0.01, 0.0001 и т.п.

В задании дана контрольная формула, позволяющая проверить правильность вычислений. Значения суммы ряда и контрольной формулы должны совпадать с учётом заданной точности. Например, если ввести точность 0.0001, то первые три знака после десятичной точки должны совпадать, а четвёртый может отличаться на 1. Впрочем, многое зависит от самого ряда и введённого значения x. Однако при точности 0.0001 разница между значениями суммы и контрольной формулы ни в коем случае не должна быть 0.1 или тем более 2.

Выводите значения суммы и контрольной формулы на разных строках строго друг под другом – так их проще сравнивать.