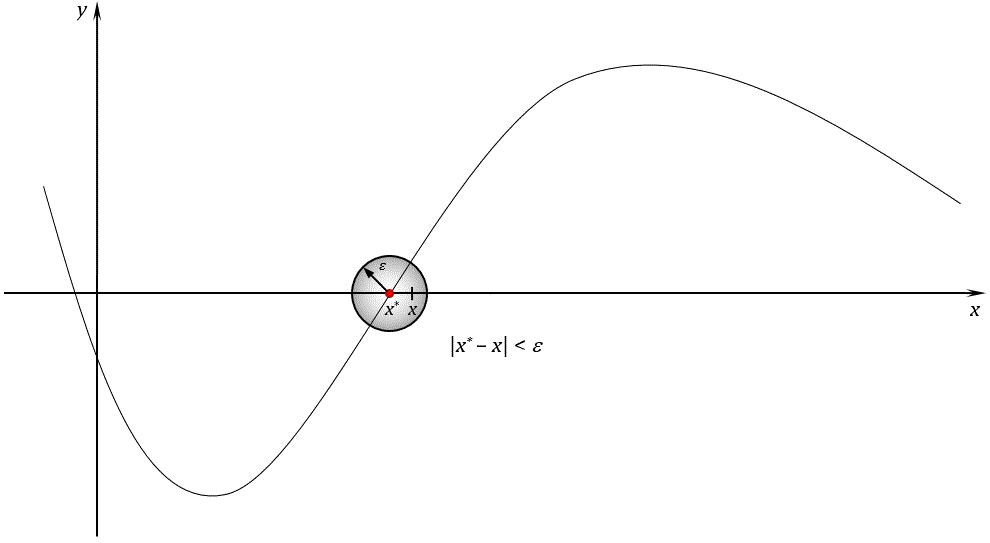
Корнем уравнения f(x) = 0 является такое, возможно не единственное, значение x = x^*, при котором имеет место тождество f(x^*) = 0. Для сложных функций не существует методов точного нахождения корня, но существуют методы приближённого вычисления корня с заданной точностью. Найти корень с заданной точностью – значит найти такое приближенное значение корня x, которое мало отличается от точного значения корня x^*, так что выполняется неравенство |x^* – x| < ε, где ε – малая положительная величина (см. рис. 1).

Рис. 1. Точное и приближённое значения корня уравнения

1. Метод простых итераций

Приведём уравнение f(x) = 0 при помощи некоторых тождественных преобразований к виду x = φ(x). Такое преобразование можно произвести разными способами, и при этом будут получаться разные функции φ(x) в правой части уравнения. Уравнение f(x) = 0 эквивалентно уравнению x = λ(x)∙f(x) + x при любой функции λ(x) ≠ 0. Таким образом, можно взять φ(x) = λ(x)∙f(x) и при этом выбрать функцию λ(x) ≠ 0 так, чтобы функция φ(x) удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения корня уравнения. В простейшем случае в качестве λ(x) выбирается неравная 0 постоянная, того же знака, что и производная в окрестностях корня. Этот вариант удобен с точки зрения задания в программе функции λ(x) и, в то же время, позволяет подобрать такое значение постоянной, которое обеспечит быстрое и точное нахождение корня уравнения.

Для нахождения корня уравнения x = φ(x) выберем какое-либо начальное приближение x₀ (расположенное, по возможности, близко к корню x^*). Далее будем вычислять последующие приближения x₁, x₂, …, x_i, x_{i + 1}, … по формуле x_{i + 1} = φ(x_i).

Заметим следующее: тот факт, что x^* – корень уравнения x = φ(x), означает, что x^* есть абсцисса точки пересечения графика y = φ(x) с прямой y = x. Если при каком-либо x_i вычислено значение x_{i + 1} = φ(x_i) и взято в качестве нового аргумента функции, то это означает, что через точку графика (x_i, φ(x_i)) проводится горизонталь до прямой y = x, а оттуда опускается перпендикуляр на ось x. Там и будет находиться новый аргумент x_{i + 1}.

Для метода простых итераций необходимо одно начальное приближение, в качестве которого можно взять середину отрезка [a, b]. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |x_{i + 1} – x_i| < ε, где ε – заданная точность вычисления. Рис. 2 иллюстрирует метод простых итераций.

Рис. 2. Метод простых итераций

Метод простых итераций сходится к корню уравнения при условии, что функция φ(x) в окрестностях корня уравнения не изменяется слишком быстро, т.е. график функции не сильно отклонён от горизонтальной прямой. Введение коэффициента λ(x) позволяет обеспечить желаемое поведение функции φ(x).

Формальное описание метода простых итераций
repeat   <сохраняем старое приближение>   <вычисляем новое приближение> until <разность между двумя текущими приближениями меньше точности>;

2. Метод секущих

Для метода секущих необходимы два начальных приближения x₁ и x₂, в качестве которых берутся границы исходного отрезка [a, b]. Используя эти два приближения, находим третье приближение x₃ как точку пересечения прямой, проведенной между точками (x₁, f(x₁)) и (x₂, f(x₂)), с осью x по следующей формуле:
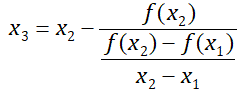или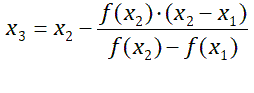

После этого самая старая точка x₁ отбрасывается, и в качестве следующих приближений берутся точки x₂ и x₃ по следующему правилу: x₁ = x₂, x₂ = x₃. После чего снова вычисляется следующее приближение по приведённой выше формуле. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |x₁ – x₂| < ε. Рис. 3 иллюстрирует метод секущих.

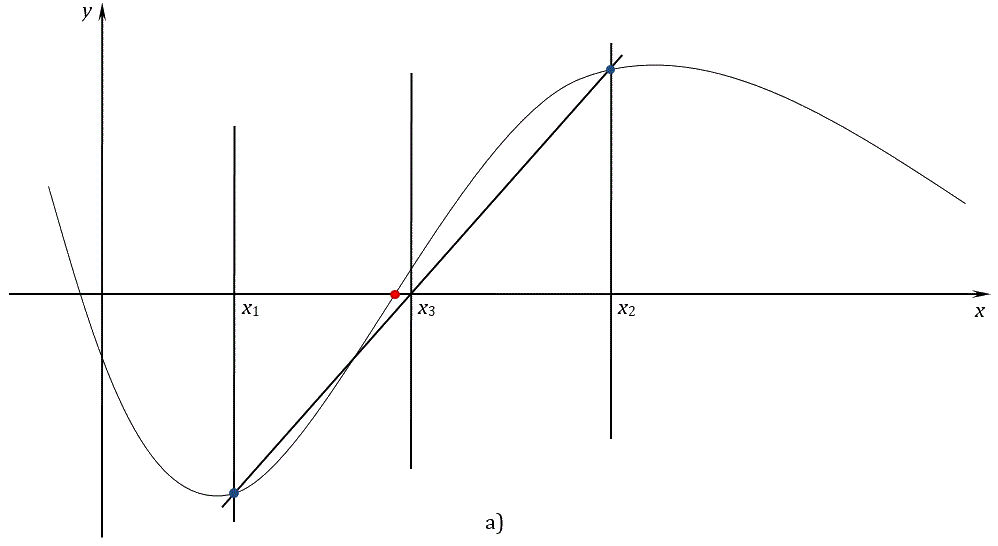
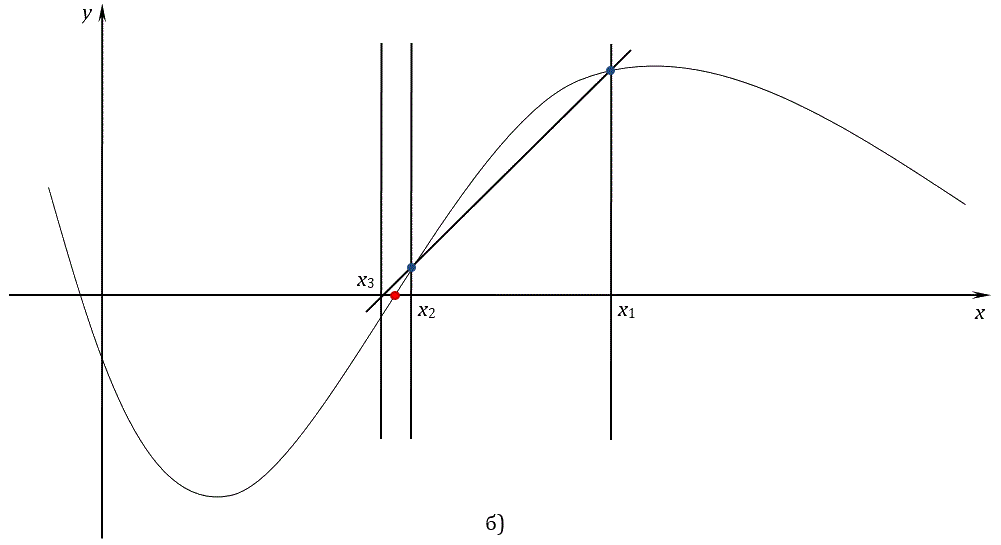
Рис. 3. Метод секущих

Метод секущих обычно сходится достаточно быстро, но чувствителен к выбору начального приближения. Для метода секущих требуется, чтобы производная функции на отрезке, ограниченном начальными приближениями, не менялась слишком быстро, иначе метод начнёт расходиться, т.е. каждое следующее приближение будет удаляться от корня уравнения.

Формальное описание метода секущих
repeat <вычислить очередное приближение на основе первых двух> <отбросить самое старое приближение> until <разность между двумя текущими приближениями меньше точности>;

3. Метод Ньютона

Пусть имеется x₀ – начальное приближение к корню уравнения f(x) = 0. Проведём касательную к графику y = f(x) в точке с координатами (x₀, f(x₀)). Новоё приближение к корню получим как точку пересечения этой касательной с осью абсцисс. Это правило приводит к следующей расчётной формуле: .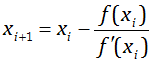

Для вычисления входящей в форму производной f´(x) можно воспользоваться выражением для её приближённого вычисления при малом значении ε: .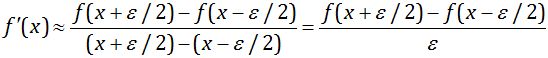

Для метода Ньютона необходимо одно начальное приближение, в качестве которого можно взять середину отрезка [a, b]. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |x_{i + 1} – x_i| < ε, где ε – заданная точность вычисления. Эта же величина ε используется для приближённого вычисления производной. Рис. 4 иллюстрирует метод Ньютона.

Рис. 4. Метод Ньютона

Метод Ньютона является наиболее быстрым среди численных методов вычисления корня уравнения. На практике необходимая точность достигается буквально после выполнения нескольких итераций.

Формальное описание метода Ньютона
repeat <сохраняем старое приближение> <вычисляем новое приближение> until <разность между двумя текущими приближениями меньше точности>;

4. Использование итерационных циклов в методах поиска корней уравнения

Мы видим, что в алгоритмах поиска корней уравнения так же, как и при нахождении суммы ряда, невозможно заранее определить, сколько итераций потребуется для нахождения корня. Это зависит от заданных начальных приближений, от точности и, конечно, от самой функции. Поэтому мы снова должны использовать циклы с неизвестным количеством повторов тела цикла. В описании метода деления отрезка пополам использовался цикл «пока», а в описании метода секущих – цикл «до». Однако это не является жёстким правилом, в любом методе можно использовать любой цикл. Главное, надо помнить, что цикл «пока» продолжается при истинности условия, а цикл «до» завершается при истинности условия. Поэтому при замене одного цикла на другой необходимо также поменять условие на противоположное.