Если показать человеку 5-10 чисел, он легко найдёт среди них максимальное. Обычно для этого достаточно одного взгляда. Набор чисел воспринимается интегрально, как единое целое, и определить максимум получается несложно. Однако если показать человеку 100-1000 чисел, он не сможет охватить их одним взглядом, и для того чтобы найти максимальное число, будет вынужден перебирать числа по одному.
Компьютер также не способен обработать весь массив целиком, поэтому алгоритмы обработки массивов разрабатываются с учётом того, что компьютер обрабатывает элементы последовательно по одному. В принципе, можно, конечно, обрабатывать два соседних элемента, или первый и последний, второй и предпоследний и т.д., но на общую идею это не влияет. Массив можно представить как стопку карточек, на каждой из которых записан один элемент массива, и в каждый момент времени доступна только одна карточка. Однако кроме самого элемента массива доступны другие карточки-переменные, куда можно делать записи.
Что же мы будет делать, если надо найти максимальный элемент массива, представленного стопкой карточек? Берётся дополнительная карточка. Первый элемент массива не с чем сравнивать, поэтому предполагается, что он является максимальным и просто переписывается на дополнительную карточку. Второй элемент массива сравнивается с числом, записанным на дополнительной карточке. Если элемент массива больше числа, записанного на дополнительной карточке, то очевидно, что это число не может быть максимальным в массиве. Поэтому число на дополнительной карточке зачёркивается и вместо него записывается второй элемент массива. Если же второй элемент массива меньше числа, записанного на дополнительной карточке, то он игнорируется, т.к. не может являться максимальным в массиве. Далее третий элемент массива сравнивается с числом, которое окажется на дополнительной карточке после обработки второго элемента массива, и опять новое число на карточку записывается только в том случае, если оно больше записанного на дополнительной карточке. Таким образом, число на дополнительной карточке может только увеличиваться и после обработки всего массива на дополнительной карточке окажется максимальный элемент массива.
Рассмотрим пример.
Массив: 2 3 5 -1 0 7 4 1
| Номер элемента массива | Элемент массива | Дополнительная карточка | |
| Инициализация | 1 | 2 | 2 |
| Цикл | 2 | 3 | 3 |
| 3 | 5 | 5 | |
| 4 | -1 | 5 | |
| 5 | 0 | 5 | |
| 6 | 7 | 7 | |
| 7 | 4 | 7 | |
| 8 | 1 | 7 |
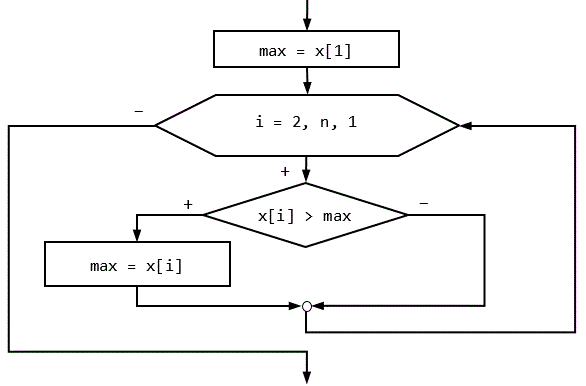
Алгоритм не зависит от исполнителя. Главное – записать его в терминах, понятных этому исполнителю. Для компьютера надо записать разработанный алгоритм на формальном языке – языке программирования. Дополнительная карточка становится переменной – назовём её max. Первый элемент массива обрабатывается отдельно, а все остальные – в цикле. Для одномерного массива цикл можно начать со второго элемента.
Алгоритм поиска минимального элемента отличается от алгоритма поиска максимального элемента только знаком в условии – вместо «больше» используется «меньше». Всё просто!
При необходимости найти номер максимального элемента кроме самого элемента массива должен, естественно, записываться и искомый номер. Для этого используется ещё одна переменная. Важно то, что переменная, хранящая номер, меняется только вместе с переменной, хранящей сам максимальный элемент, – до цикла осуществляется инициализации обеих переменных, а в теле цикла обе переменные меняются при выполнении условия.
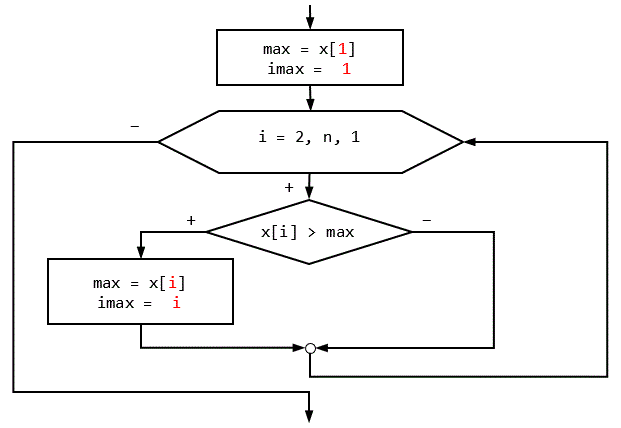
Понятно, что номер минимального элемента ищется аналогично, только опять в сравнении используется другой знак.
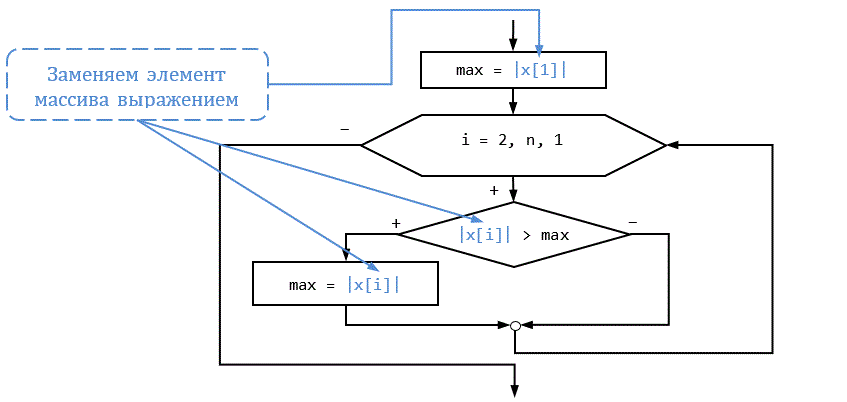
Часто бывает необходимо найти максимальное или минимальное значение не среди элементов массива, а среди множества значений, которые являются некоторой функцией, зависящей от элементов массива или нескольких массивов, например, надо найти максимальный по модулю элемент или минимальную разность элементов двух массивов с одинаковыми номерами a[i] – b[i]. Ничего сложного тут нет – надо просто во всех точках, где используется элемент массива поставить выражение, экстремальное значение которого надо найти. Элемент массива в алгоритме поиска экстремального значения используется три раза – при инициализации, в сравнении и при присвоении нового значения в случае выполнения условия.
Рассмотрим для примера поиск максимального по модулю элемента массива.
Пусть надо найти наибольшую среди сумм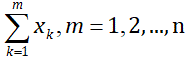 
. В данном случае невозможно просто подставить вместо элемента массива выражение, т.к. значение выражения надо искать с использованием цикла. Первое, что приходит в голову, – сформировать массив из этих сумм.
for m := 1 to n do
for k := 1 to m do
...
Однако использовать для этого цикл в цикле не разумно, т.к. каждая сумма может быть выражена через предыдущую.
s1 = x1
s2 = x1 + x2
s3 = x1 + x2 + x3
s4 = x1 + x2 + x3 + x4
…
Мы видим, что каждая последующая сумма содержит те же слагаемые, что и предыдущая, плюс одно слагаемое. Значит, каждую сумму можно выразить через предыдущую следующим образом:
s1 = x1
s2 = s1 + x2
s3 = s2 + x3
s4 = s3 + x4
…
Теперь мы видим, что для подсчёта всех сумм можно использовать один цикл:
s[1] := x[1];
for i := 2 to n do
s[i] := s[i-1] + x[i];
А теперь можно объединить циклы для поиска суммы и для поиска максимума в один и избавится от массива сумм – использовать простую переменную, к старому значению это переменной прибавлять очередной элемент массива и тут же полученную сумму сравнивать с максимальной.
Алгоритм поиска экстремального значения в матрице ничем принципиальным не отличается от алгоритма поиска экстремального значения в одномерном массиве, кроме, естественно, того, что для обработки матрицы надо использовать два цикла. Но для матрицы нельзя использовать число 2 как начальное значение счётчиков цикла, т.к. в этом случае не будет обрабатываться первая строка и/или первый столбец. Можно, конечно, написать отдельные циклы для их обработки, но это не имеет смысла.
При тестировании программ поиска экстремального элемента необходимо, как и в других случаях, найти некоторые критические точки. Для таких программ это место расположения экстремального элемента – в начале, в конце или в середине массива.
Задание. Разработать алгоритм поиска количества максимальных элементов.
Задание. Разработать алгоритм поиска номера первого минимального элемента и номера последнего минимального элемента.