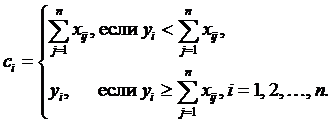Разработать программу для обработки двух матриц разного размера с использованием процедур и функций, реализованных в отдельном модуле. Кроме процедур ввода/вывода при разработке программы необходимо выделить две или три подпрограммы и выбрать подходящий тип этих подпрограмм – процедура или функция. Ввод всех данных осуществляется из файла, вывод – в файл. Для передачи имён файлов должны использоваться параметры программы.
Кроме матриц могут быть также заданы два одномерных массива.
Функция f, применяемая к элементам матриц, передаётся в подпрограмму с помощью функционального типа. Задание необходимо выполнить для двух вариантов функции f – в качестве первого варианта берём f(x) = x для того, чтобы было легко проверить правильность работы программы, в качестве второго – любую другую функцию одного аргумента (например, sin(x) + cos(x) или x2 – 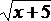 ). В случае равенства вычисленных значений выводить соответствующее сообщение и не осуществлять никакой обработки.
). В случае равенства вычисленных значений выводить соответствующее сообщение и не осуществлять никакой обработки.