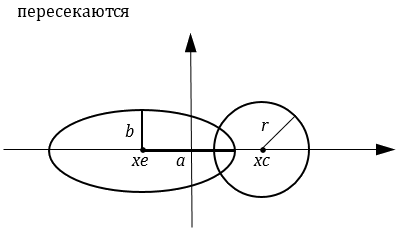
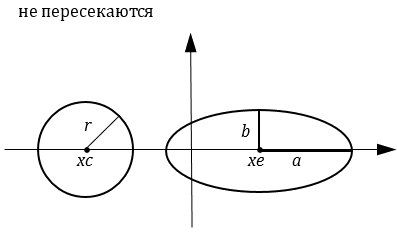
Постановка задачи. Разработать программу для определения взаимного расположения (концентричность, вложенность, касание, пересечение/не пересечение) двух заданных фигур – круга и эллипса.
Шаг 1. Уточнение постановки задачи
Для упрощения задачи будем считать, что центр круга и центр эллипса находятся на оси x, т.е. y-координата центра равна 0. Кроме того, будем считать, что полуоси эллипса параллельны осям координат.
 |
 |
 |
 |
 |
 |
Шаг 2. Общая структура программы
Программа на процедурном языке программирования состоит из данных и действий по их обработке.
program Geometry;
{ Описание данных – констант, типов и переменных }
begin
{ Обработка данных }
end.
Шаг 3. Разработка структуры данных
Чтобы геометрические фигуры можно было обработать в программе, необходимо задать для каждой из них некоторый набор данных, однозначно определяющий эту фигуру. Для круга это будут x-координата центра и радиус, для эллипса – x-координата центра и длины полуосей.
program Geometry;
var
{ Входные данные }
xc, r: real; { вещ xc - координата центра круга, вещ r - радиус круга }
xe, a, b: real; { вещ xe - координата центра эллипса, вещ a, b - полуоси эллипса }
{ Выходные данные }
{ Сообщение 'Фигуры концентричны', 'Круг вложен в эллипс', 'Эллипс вложен в круг', 'Фигуры касаются',
'Фигуры пересекаются' или 'Фигуры не пересекаются' }
begin
{ Обработка данных }
end.
Шаг 4 . Разработка тестов
| № теста | Входные данные | Ожидаемые результаты | Смысл теста |
|---|---|---|---|
| 1 |
xc = 0 r = 1.3 xe = 0 a = 3.3, b = 2.2 |
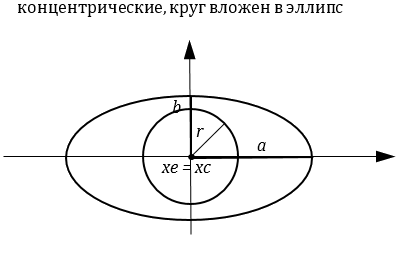
Фигуры концентричны, круг вложен в эллипс |
Подбираем координаты центров и радиусы/полуоси так, чтобы получались разные результаты. |
| 2 |
xc = 0 r = 5.5 xe = 0 a = 4.2, b = 2.8 |
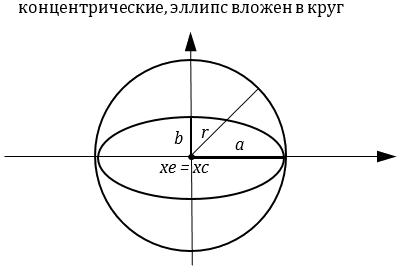
Фигуры концентричны, эллипс вложен в круг |
|
| 3 |
xc = 1 r = 2.7 xe = 1 a = 2.3, b = 3.2 |
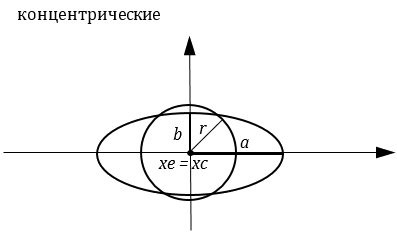
Фигуры концентричны | |
| 4 |
xc = 2 r = 1 xe = -1 a = 2, b = 1.2 |
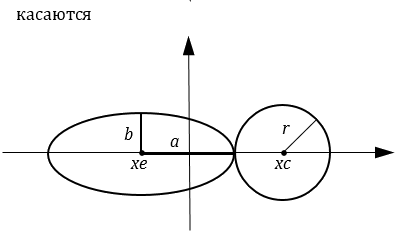
Фигуры касаются | |
| 5 |
xc = 0 r = 2.5 xe = 4 a = 3, b = 2 |
Фигуры пересекаются | |
| 6 |
xc = 5 r = 5.7 xe = 2 a = 2, b = 0.8 |
Фигуры пересекаются | |
| 7 |
xc = 5 r = 3.3 xe = -4 a = 2, b = 4 |
Фигуры не пересекаются | |
| 8 |
xc = 0 r = 2.5 xe = 4 a = 1, b = 3 |
Фигуры не пересекаются |
Шаг 5. Разработка общей структуры программы
Программа должна состять из трёх основных частей – ввод исходных данных, получение результатов, вывод полученных результатов. В общем случае эти части должны выполняться последовательно. Но в данном случае трудно разделить получение результатов и вывод. В принципе, можно сформировать переменную перечислимого типа, которая будет принимать одно из нескольких значение в соответствии с расположением фигур, и затем выводить нужное сообщение в зависимости от значения этой переменной. Но в данном случае это лишь увеличит размер программы.
program Geometry;
var
{ Входные данные }
xc, r: real; { вещ xc - координата центра круга, вещ r - радиус круга }
xe, a, b: real; { вещ xe - координата центра эллипса, вещ a, b - полуоси эллипса }
{ Выходные данные }
{ Сообщение 'Фигуры концентричны', 'Круг вложен в эллипс', 'Эллипс вложен в круг', 'Фигуры касаются',
'Фигуры пересекаются' или 'Фигуры не пересекаются' }
begin
{ Ввод исходных данных }
{ Проверка пересечения фигур и вывод результата }
end.
Шаг 6. Разработка ввода исходных данных
Собственно ввод осуществляется оператором read или readln. Но желательно выводить подсказки, чтобы было понятно, что именно нужно ввести. Вывод осуществляется оператором write или writeln.
Входная форма 
program Geometry;
var
{ Входные данные }
xc, r: real; { вещ xc - координата центра круга, вещ r - радиус круга }
xe, a, b: real; { вещ xe - координата центра эллипса, вещ a, b - полуоси эллипса }
{ Выходные данные }
{ Сообщение 'Фигуры концентричны', 'Круг вложен в эллипс', 'Эллипс вложен в круг', 'Фигуры касаются',
'Фигуры пересекаются' или 'Фигуры не пересекаются' }
begin
{ Ввод исходных данных }
write('Введите координату центра круга и радиус круга: ');
readln(xc, r);
write('Введите координату центра эллипса и полуоси эллипса: ');
readln(xe, a, b);
{ Проверка пересечения фигур и вывод результата }
end.
Шаг 7 . Разработка вычислительной части программы
Опишем метод решения задачи. Если центр круга и центр эллипса совпадают, то фигуры концентричны. При этом если радиус круга меньше обеих полуосей эллипса, то круг вложен в эллипс, а если радиус круга больше обеих полуосей эллипса, то эллипс вложен в круг (можно использовать операции «меньше или равно» и «больше или равно»). Если расстояние между центрами круга и эллипса равно сумме длин радиуса круга и полуоси эллипса a, то фигуры касаются. Если расстояние между центрами круга и эллипса меньше суммы длин радиуса круга и полуоси эллипса a, то фигуры пересекаются. В противном случае фигуры не пересекаются.
program Geometry;
var
{ Входные данные }
xc, r: real; { вещ xc - координата центра круга, вещ r - радиус круга }
xe, a, b: real; { вещ xe - координата центра эллипса, вещ a, b - полуоси эллипса }
{ Выходные данные }
{ Сообщение 'Фигуры концентричны', 'Круг вложен в эллипс', 'Эллипс вложен в круг', 'Фигуры касаются',
'Фигуры пересекаются' или 'Фигуры не пересекаются' }
begin
{ Ввод исходных данных }
writeln('Введите координату центра круга и радиус круга');
readln(xc, r);
writeln('Введите координату центра эллипса и полуоси эллипса');
readln(xe, a, b);
{ Проверка пересечения фигур и вывод результата }
if xe = xc then
begin
writeln('Фигуры концентричны');
if (r <= a) and (r <= b) then
writeln('Круг вложен в эллипс')
else if (r >= a) and (r >= b) then
writeln('Эллипс вложен в круг');
end
else if abs(xc - xe) = r + a then
writeln('Фигуры касаются')
else if abs(xc - xe) < r + a then
writeln('Фигуры пересекаются')
else
writeln('Фигуры не пересекаются');
end.