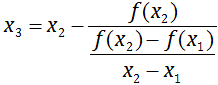 или
или 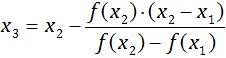
Разработать программу для приближённого нахождения корня уравнения f(x) = 0 для нескольких (не менее 5) функций. Функции f(x) берутся из задачника – лабораторный практикум по курсу «Основы программирования», лабораторная работа № 5. Номер функции вводится. Для выбора функции не использовать операторы выбора if и case.
Корень уравнения находится тремя методами – методом секущих, методом простых итераций и методом Ньютона. Функция, для которой ищется корень, передаётся в процедуру, реализующую метод нахождения корня, с помощью функционального типа.
Для определения начального приближения необходимо построить график функции.
Корень уравнения определяется с заданной точностью ε. Для каждого метода нужно также считать количество итераций, необходимых для вычисления корня. Осуществлять выход из цикла, когда количество итераций превышает заданное значение. Количество итераций передавать в основную программу по желанию пользователя через параметр типа указатель на целое со значением по умолчанию, равным nil.
В качестве результата нужно вывести значение корня, значение функции в корне и количество итераций или сообщение о том, что превышено максимально допустимое количество итераций. Количество знаков после десятичной точки должно соответствовать введённой точности.
Осуществлять проверку аномалий. Для завершения выполения программы можно использовать операцию exit.
Методы поиска корня уравнения реализовать в отдельном модуле.
| Класс | Имя | Смысл | Тип | Структура | Диапазон |
|---|---|---|---|---|---|
| Входные данные | x1, x2 | Начальные приближения | вещ. | простая переменная | |
| e | Точность вычислений | вещ. | простая переменная | 0 < e < 1 | |
| f | Функция, задающая уравнение | функциональный | простая переменная | ||
| Выходные данные | x | Корень уравнения | вещ. | простая переменная | |
| p | Количество итераций | указатель на целое | простая переменная |
| Класс | Имя | Смысл | Тип | Структура | Диапазон |
|---|---|---|---|---|---|
| Входные данные | x0 | Начальное приближение | вещ. | простая переменная | |
| factor | Коэффициент | вещ. | простая переменная | -1 < factor < 1 | |
| e | Точность вычислений | вещ. | простая переменная | 0 < e < 1 | |
| f | Функция, задающая уравнение | функциональный | простая переменная | ||
| Выходные данные | x | Корень уравнения | вещ. | простая переменная | |
| p | Количество итераций | указатель на целое | простая переменная |
| Класс | Имя | Смысл | Тип | Структура | Диапазон |
|---|---|---|---|---|---|
| Входные данные | x0 | Начальное приближение | вещ. | простая переменная | |
| e | Точность вычислений | вещ. | простая переменная | 0 < e < 1 | |
| f | Функция, задающая уравнение | функциональный | простая переменная | ||
| Выходные данные | x | Корень уравнения | вещ. | простая переменная | |
| p | Количество итераций | указатель на целое | простая переменная |
Исходные данные для методов поиска корня уравнения определяются по графику функции.
Для метода секущих необходимы два начальных приближения x1 и x2, в качестве которых берутся границы исходного отрезка [a, b]. Используя эти два приближения, находим третье приближение x3 как точку пересечения прямой, проведенной между точками (x1, f(x1)) и (x2, f(x2)), с осью x по следующей формуле:
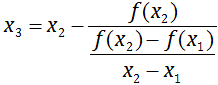 или
или 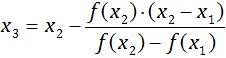
После этого самая старая точка x1 отбрасывается, и в качестве следующих приближений берутся точки x2 и x3 по следующему правилу: x1 = x2, x2 = x3. После чего снова вычисляется следующее приближение по приведённой выше формуле. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |x1 – x2| < ε. Рис. 1 иллюстрирует метод секущих.


Рис. 1. Метод секущих
Метод секущих обычно сходится достаточно быстро, но он чувствителен к выбору начального приближения. Для метода секущих требуется, чтобы производная функции на отрезке, ограниченном начальными приближениями, не менялась слишком быстро, иначе метод начнёт расходиться, т.е. каждое следующее приближение будет удаляться от корня уравнения.
Формальное описание метода секущих
repeat
<вычислить очередное приближение на основе первых двух>
<отбросить самое старое приближение>
until <разность между двумя текущими приближениями меньше точности> or <количество итераций больше порогового значения>;
Приведём уравнение f(x) = 0 при помощи некоторых тождественных преобразований к виду x = φ(x). Такое преобразование можно произвести разными способами, и при этом будут получаться разные функции φ(x) в правой части уравнения. Уравнение f(x) = 0 эквивалентно уравнению x = λ(x)∙f(x) при любой функции λ(x) ≠ 0. Таким образом, можно взять φ(x) = λ(x)∙f(x) и при этом выбрать функцию λ(x) ≠ 0 так, чтобы функция φ(x) удовлетворяла тем свойствам, которые понадобятся нам для обеспечения нахождения корня уравнения. В простейшем случае в качестве λ(x) выбирается неравная 0 постоянная. Этот вариант удобен с точки зрения задания в программе функции λ(x) и, в то же время, позволяет подобрать такое значение постоянной, которое обеспечит быстрое и точное нахождение корня уравнения.
Для нахождения корня уравнения x = φ(x) выберем какое-либо начальное приближение x0 (расположенное, по возможности, близко к корню x*). Далее будем вычислять последующие приближения x1, x2, …, xi, xi + 1, … по формуле xi + 1 = φ(xi).
Заметим следующее: тот факт, что x* – корень уравнения x = φ(x), означает, что x* есть абсцисса точки пересечения графика y = φ(x) с прямой y = x. Если при каком-либо xi вычислено значение xi + 1 = φ(xi) и взято в качестве нового аргумента функции, то это означает, что через точку графика (xi, φ(xi)) проводится горизонталь до прямой y = x, а оттуда опускается перпендикуляр на ось x. Там и будет находиться новый аргумент xi + 1.
Для метода простых итераций необходимо одно начальное приближение, в качестве которого можно взять середину отрезка [a, b]. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |xi + 1 – xi| < ε, где ε – заданная точность вычисления. Рис. 2 иллюстрирует метод простых итераций.

Рис. 2. Метод простых итераций
Метод простых итераций сходится к корню уравнения при условии, что функция φ(x) в окрестностях корня уравнения не изменяется слишком быстро, т.е. график функции не сильно отклонён от горизонтальной прямой. Введение коэффициента λ(x) позволяет обеспечить желаемое поведение функции φ(x). В простейшем случае в качестве коэффициента λ(x) можно взять константу, лежащую в пределах от -1 до 1.
Формальное описание метода простых итераций
repeat
<сохраняем старое приближение>
<вычисляем новое приближение>
until <разность между двумя текущими приближениями меньше точности> or <количество итераций больше порогового значения>;
Пусть имеется x0 – начальное приближение к корню уравнения f(x) = 0. Проведём касательную к графику y = f(x) в точке с координатами (x0, f(x0)). Новоё приближение к корню получим как точку пересечения этой касательной с осью абсцисс. Это правило приводит к следующей расчётной формуле: 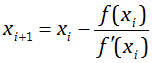 .
.
Для вычисления входящей в форму производной f´(x) можно воспользоваться выражением для её приближённого вычисления при малом значении ε: 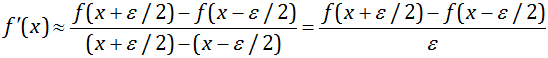 .
.
Для метода Ньютона необходимо одно начальное приближение, в качестве которого можно взять середину отрезка [a, b]. Процесс вычисления прекращается, когда разность между двумя текущими приближениями становится меньше точности, т.е. когда выполняется условие |xi + 1 – xi| < ε, где ε – заданная точность вычисления. Эта же величина ε используется для приближённого вычисления производной. Рис. 3 иллюстрирует метод Ньютона.

Рис. 3. Метод Ньютона
Метод Ньютона является наиболее быстрым среди численных методов вычисления корня уравнения. На практике необходимая точность достигается буквально после выполнения нескольких итераций.
Формальное описание метода Ньютона
repeat
<сохраняем старое приближение>
<вычисляем новое приближение>
until <разность между двумя текущими приближениями меньше точности> or <количество итераций больше порогового значения>;
Прежде всего необходимо объявить параметр типа указатель на целое со значением по умолчанию, равным nil. Для объявления указателя используется знак ^, после него пишется тип. Значение по умолчанию указывается сразу после типа параметра.
function Iterations(x0, e, factor: real; f: func; p: ^integer := nil): real;
В функции объявляем локальную переменную для подсчёта количества итераций, например, n. Используем эту переменную для проверки превышения порогового значения. После нахождение корня присваиваем значение переменной n переменной, адрес которой хранится в указателе p, но только если p не равно nil.
if p <> nil then
p^ := n;
В основной программе вводим символьную переменную, которая определяет необходимость передачи и вывода количества итераций. Если пользователь хочет узнать количество итераций, передаём в функцию Iterations адрес какой-либо переменной с помощью выражения @<имя переменной> (@ – операция получения адреса переменной). Если пользователь не хочет узнать количество итераций, передаём только четыре фактических параметра. В качестве пятого компилятор сам подставит значение по умолчанию.