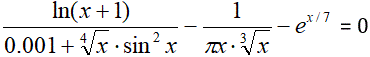на отрезке [a, b] с заданной точностью e. Корень уравнения находится двумя методами – методом деления отрезка пополам и методом простых итераций.
Постановка задачи. Разработать программу для приближенного нахождения корня уравнения 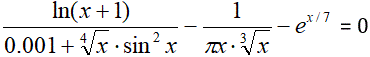на отрезке [a, b] с заданной точностью e. Корень уравнения находится двумя методами – методом деления отрезка пополам и методом простых итераций.
Шаг 1. Общая структура программы
Программа на процедурном языке программирования состоит из данных и действий по их обработке.
program Root;
{ Описание данных – констант, типов и переменных }
begin
{ Обработка данных }
end.
Шаг 2. Разработка структуры данных
Из постановки задачи видно, что задаются границы отрезка a и b и точность e и надо найти корень уравнения x.
program Root;
var
{ Входные данные }
a, b, e: real; { вещ a, b - границы отрезка, вещ e - точность }
{ Выходные данные }
x: real; { вещ x - корень уравнения }
begin
{ Обработка данных }
end.
Шаг 3. Разработка тестов
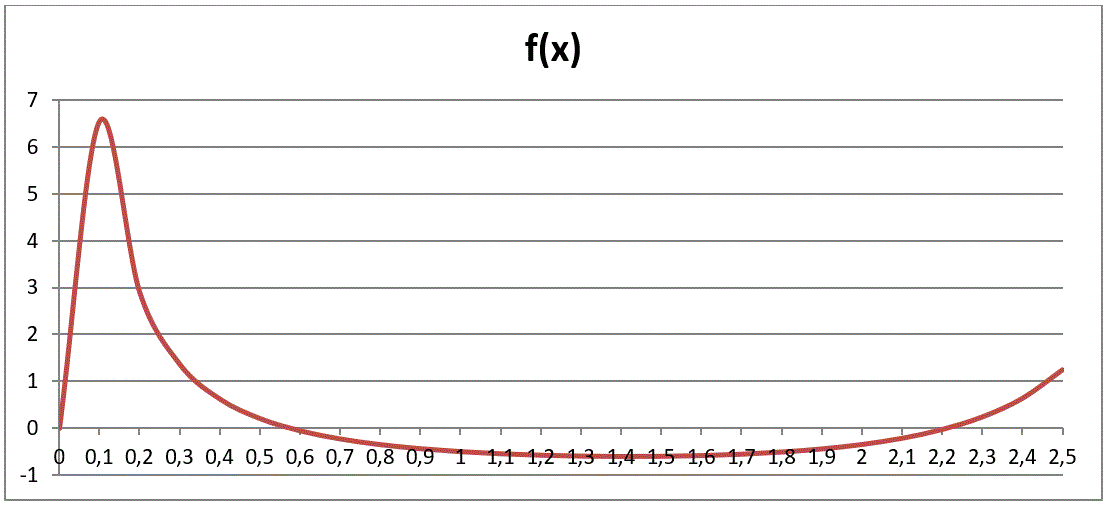
По данному графику видно, что уравнение имеет два корня (как минимум) – один примерно равен 0.6, а другой примерно равен 2.2. Таким образом, можно использовать, например, следующие отрезки – [0.1; 1] и [1.5; 2.5]. Правильность полученного результата проверяем по значению функции в корне – оно должно быть примерно равно 0 (зависит от введённой точности).
Шаг 4. Разработка общей структуры программы
Программа должна состять из трёх основных частей – ввод исходных данных, получение результатов, вывод полученных результатов. Поскольку в данной работе нужно найти корень уравнения двумя методами, получение результатов и вывод будут программироваться дважды.
program Root;
var
{ Входные данные }
a, b, e: real; { вещ a, b - границы отрезка, вещ e - точность }
{ Выходные данные }
x: real; { вещ x - корень уравнения }
begin
{ Ввод исходных данных }
{ Вычисление корня методом деления отрезка пополам }
{ Вывод результатов, полученных по методу деления отрезка пополам }
{ Вычисление корня методом простых итераций }
{ Вывод результатов, полученных по методу простых итераций }
end.
Шаг 5. Разработка ввода и вывода
Запрограммируем ввод и вывод согласно входной и выходной форме. Для проверки вывода напишем заглушку, которая будет присваивать переменной x значение середины отрезка. При выводе вместо значения f(x) пока тоже будем выводить значение переменной x.
Входная форма 
Выходная форма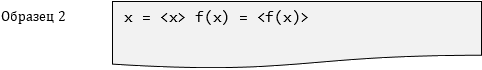 
program Root;
var
{ Входные данные }
a, b, e: real; { вещ a, b - границы отрезка, вещ e - точность }
{ Выходные данные }
x: real; { вещ x - корень уравнения }
begin
{ Ввод исходных данных }
write('Введите границы отрезка: ');
readln(a, b);
write('Введите точность: ');
readln(e);
{ Вычисление корня методом деления отрезка пополам – заглушка }
x := (a + b) / 2;
{ Вывод результатов, полученных по методу деления отрезка пополам }
writeln('x = ', x, ' f(x) = ', x);
{ Вычисление корня методом простых итераций – заглушка }
x := (a + b) / 2;
{ Вывод результатов, полученных по методу простых итераций }
writeln('x = ', x, ' f(x) = ', x);
end.
Шаг 6. Разработка функции, для которой вычисляется корень
При вычислении корня, а также при выводе, нам придётся несколько раз вычислять значение функции. Чтобы не вставлять в текст программы громоздкое математическое выражение, можно реализовать математическую функцию через программную функцию. Собственно, понятие функции в программировании эквивалентно математическому понятию функции - на вход функции подаётся одно или несколько значений, на выходе получается некоторый результат.
Для задания функции в программе необходимо указать её имя, имена и типы параметров (в данном случае нам потребуется один вещественный параметр), тип результата (в данном случае тоже вещественный) и определить, что именно делает функция.
Реализуем нашу функцию и изменим вывод так, чтобы выводилось значение f(x). Для проверки правильность задания функции можно полученные результаты сравнивать со значениями на построенном графике функции.
program Root;
var
{ Входные данные }
a, b, e: real; { вещ a, b - границы отрезка, вещ e - точность }
{ Выходные данные }
x: real; { вещ x - корень уравнения }
{ Функция, описывающая уравнение, для которого ищется корень }
function f(x: real): real;
begin
f := ln(x + 1) / (0.001 + power(x, 0.25) * sqr(sin(x))) - 1 / (pi * x * power(x, 1 / 3)) - exp(x / 7);
end;
begin
{ Ввод исходных данных }
write('Введите границы отрезка: ');
readln(a, b);
write('Введите точность: ');
readln(e);
{ Вычисление корня методом деления отрезка пополам – заглушка }
x := (a + b) / 2;
{ Вывод результатов, полученных по методу деления отрезка пополам }
writeln('x = ', x, ' f(x) = ', f(x));
{ Вычисление корня методом простых итераций – заглушка }
x := (a + b) / 2;
{ Вывод результатов, полученных по методу простых итераций }
writeln('x = ', x, ' f(x) = ', f(x));
end.
Шаг 7. Разработка вычислительной части программы
Методы приближённого вычисления корня уравнения описаны в соответствующем практическом занятии.